入门时空序列预测
时间序列预测
时间序列预测是指使用过去的时间序列数据来预测未来的数据点。
时间序列分析的核心就是挖掘该时间序列中的自相关性。
时空序列预测
时空序列包含了时间与空间上的信息。我们在这里使用的雷达数据就是典型的时空序列。
RNN
循环神经网络(RNN)是一种简单的用于时间序列预测的神经网络模型。RNN的特点是其神经元之间存在循环连接,神经元接受输入数据以及上一个时间的隐藏状态。 \[ h_t = \sigma(W_{hh} \cdot h_{t-1} + W_{hx} \cdot x_t + b_h) y_t = W_{hy} \cdot h_t + b_y \]
梯度消失与梯度爆炸
在反向传播时,可能会经过多层的权重更新,导致梯度逐渐变小,最终趋近于零,这就是梯度消失。这种现象在 RNN 上尤其常见,因为存在循环连接时,很小的梯度会不断相乘。同样,如果梯度逐渐变大,这就是梯度爆炸。
梯度消失会导致网络的前期层几乎不更新参数,难以收敛,梯度爆炸会导致权重更新过快,破坏网络的稳定性。为了解决 RNN 中的这些问题,出现了一些改进的模型,如 LSTM。
LSTM
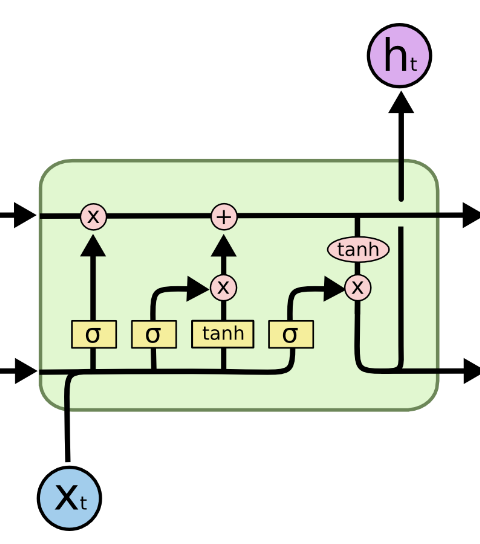
长短期记忆(LSTM)神经网络是一种特殊的 RNN。传统的 RNN 在捕捉长期依赖关系时通常表现不佳,容易出现梯度消失与梯度爆炸问题。
LSTM 的核心思想是引入了门控机制,允许网络选择性地更新和忽略隐藏状态中的信息,从而更好地控制信息的流动。一个标准的 LSTM 单元包括三个门控和一个记忆单元:
遗忘门:\(f_t=\sigma(W_{f}\cdot[h_{t-1},x_t]+b_f)\)
遗忘门的作用是决定在当前时间步是否要从记忆单元中移除信息。它通过一个 sigmoid 函数来生成一个介于 0 和 1 之间的值,来控制记忆单元中的信息保留程度。
输入门:\(i_t=\sigma(W_{i}\cdot[h_{t-1},x_t]+b_i)\)
\(\hat{c_t}=\tanh(W_c\cdot[h_{t-1},x_t]+b_c)\)
输入门决定在当前时间步要从输入数据中添加多少信息到记忆单元中。它包括一个 sigmoid 层和一个 tanh 层,用于确定更新的记忆内容。
更新门:\(c_t=f_t\circ c_{t-1}+i_t\circ \hat{c_t}\)
更新门根据遗忘门和输出门的控制,计算得到更新的内容。
输出门:\(o_t=\sigma(W_o\cdot[h_{t-1},x_t]+b_o)\)
\(h_t=o_t\circ\tanh(c_t)\)
输出门决定在当前时间步要从记忆单元中提取多少信息作为输出。它通过一个 sigmoid 层和记忆单元的内容来生成一个输出。
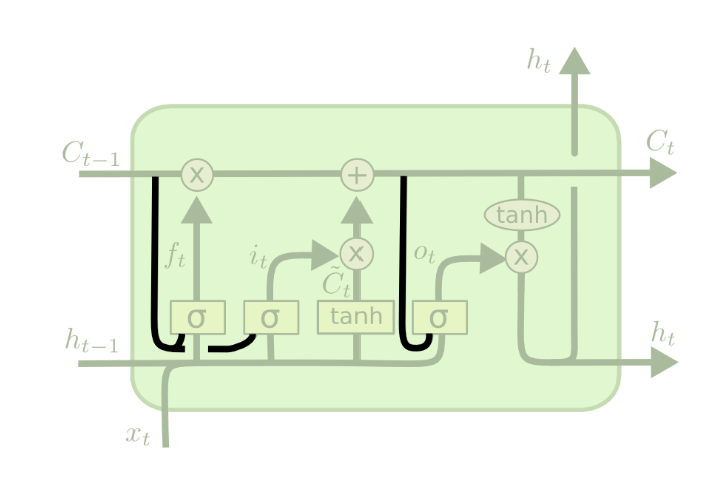
变种——增加peephole
为了进一步增强 LSTM
的建模能力,我们允许门控使用记忆单元中的内容作为输入: \[
\begin{align}
f_t&=\sigma(W_{f}\cdot[h_{t-1},x_t,c_{t-1}]+b_f)\\\\
i_t&=\sigma(W_{i}\cdot[h_{t-1},x_t,c_{t-1}]+b_i)\\\\
\hat{c_t}&=\tanh(W_c\cdot[h_{t-1},x_t,c_{t-1}]+b_c)\\\\
c_t&=f_t\circ c_{t-1}+i_t\circ \hat{c_t}\\\\
o_t&=\sigma(W_{o}\cdot[h_{t-1},x_t,c_{t-1}]+b_o)\\\\
h_t&=o_t\circ\tanh(c_t)
\end{align}
\] 
ConvLSTM
ConvLSTM 将矩阵相乘的操作更换为卷积。通过卷积操作,实现了对时空信息的特征提取。 \[ \begin{align} f_t&=\sigma(W_{f}\ast[h_{t-1},x_t,c_{t-1}]+b_f)\\\\ i_t&=\sigma(W_{i}\ast[h_{t-1},x_t,c_{t-1}]+b_i)\\\\ \hat{c_t}&=\tanh(W_c\ast[h_{t-1},x_t,c_{t-1}]+b_c)\\\\ c_t&=f_t\circ c_{t-1}+i_t\circ \hat{c_t}\\\\ o_t&=\sigma(W_{o}\ast[h_{t-1},x_t,c_{t-1}]+b_o)\\\\ h_t&=o_t\circ\tanh(c_t) \end{align} \]
Encoding Forecasting Structure
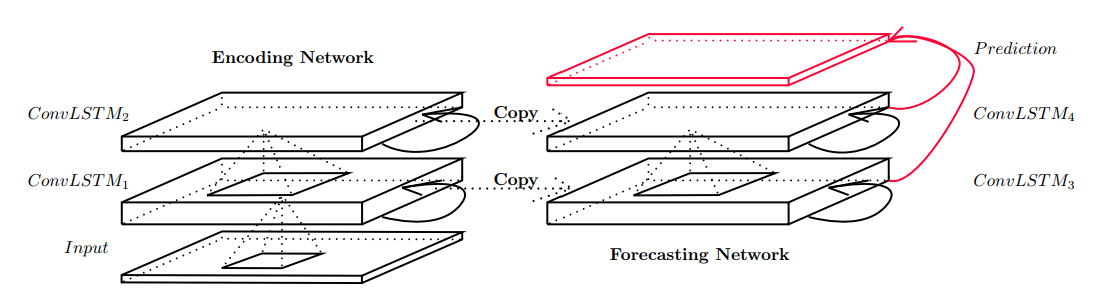
数据集
我们使用的数据是20230530的雷达数据,存储格式为。通过雷达回波数据,我们可以利用 Z-R 关系估计降水量: \[ Z=aR^b \] 其中 \(Z\) 为回波强度,\(R\) 为降水量。
此处的雷达数据中存放的回波强度单位为 dBZ,这意味着 \[ dBZ=10\lg a + 10b\lg R \] 其范围大致在 \([-20,70]\)。
另外,雷达存储的 dBZ 数据并不是严格的三维网格数据。我们通过插值的方法,将其转化为分辨率 2km 的三位网格数据,随后垂直方向取第一个通道的二维数据作为原始数据。
归一化
输入的雷达数据中有较多的缺测值,我们统一用 -20 替换。
由于所构建的模型的输出范围是\([0,1]\),我们对所有的 dBZ 都进行了如下操作: \[ P=\dfrac{dBZ+10}{70}\\\\ input=\begin{cases} 0,P<0\\\\ 1,P>1\\\\ P,else \end{cases} \] 这样我们的输入被映射到 \([0,1]\) 上,同时筛除了部分异常点。